[FC 4.31]비행기(양력)
물리/유체역학 2017. 11. 14. 10:25“비행기가 어떻게 양력을 얻을까?”는 물리의 기본적인 문제이다.
기본적인 답에는 베르누이의 원리가 있지만 그것이 유일한, 또는 중요한 요인일까?
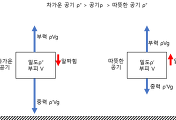
날개의 모양이(그림 4.31) 베르누이 효과를 일으키도록 만들어졌다면 어떻게 비행기가 뒤집혀서도 날 수 있을까?
근본 논쟁의 중요한 점은 공기가 날개 아래보다 위에서 빨리 흐른다는 것이다.
그리하여 베르누이 원리에 의해 압력이 날개 아래가 위보다 높아지고 따라서 양력이 생긴다.
그런데 왜 공기가 위쪽에서 빨리 흘러야 할까?
아래와 위에서 공기의 흐름이 같은 시간 내에 날개를 반드시 지나가야 한다.
위의 공기 흐름은 더 긴 거리를 지나가야 하기 때문에 빨리 흘러야 한다.
기본 논쟁의 대답은 여기서 마친다.
그러나 왜 위의 공기가 아래 공기와 같은 시간에 날개를 지나가야 할까?
이 점은 설명이 잘 안되고 있다.
사실상 위와 아래의 공기 흐름은 서로 통과 시간이 다르다.
그럼 어떻게 날개가 양력을 얻을까?
The air passing the top of the wing moves faster than the air passing below the wing. The pressure above the wing is less
than the pressure below the wing. As a result, a net upward force is on the wing.
날개 윗부분을 통과하는 공기는 날개 아래를 통과하는 공기보다 더 빨리 움직인다. 날개 위의 압력은 날개 아래의 압력보다 작다. 그 결과, 날개에는 윗방향의 알짜힘이 있다.
Whether or not the Bernoulli principle applies to the calculation of this lift is not always dear in the references. The principle is a statement of the conservation of energy (here, pressure and kinetic energy) along a stream line in the air flow.
베르누이 원리가 이 양력 계산에 적용되는지 여부는 참고 문헌에서 항상 중요한 것은 아니다. 원리는 기류에서 유선을 따른 에너지의 보존(여기에서는, 압력과 운동 에너지)에 대한 진술이다.
Since the air flow around a wing is affected by adhesion to the wing and viscosity, both of which do work on the air, the principle should not be applicable. However, it can still be used if the adhesion and viscosity are accounted for by superimposing a circulation of air (forward underneath the wing, rearward on top) on the irrotational flow of the air passing the wing.
날개 주위의 공기 흐름은 공기에서 작용하는 두가지인 날개와의 부착력과 점도에 의해 영향을 받기 때문에, 이 원리는 적용할 수 없다. 그러나 날개를 통과하는 공기의 비회전 흐름에 공기의 순환(날개 아래에서 앞쪽으로, 날개 위에서 뒤쪽으로)을 겹쳐서 접착력과 점도를 설명하는 경우에는 여전히 사용할 수 있다.
In the work of Kutta and Joukowsky on lift, such a superposition of a circulation is made. Above the wing, the circulation speed adds to the i motional speed past the wing to give a greater speed. Below the wing the circulation opposes the irrotiona! flow, and the air speed is reduced. By Bernoulli's principle, the pressure above the wing is less than that below the wing, thus there is lift. The application of the Bernoulli principle in obtaining lift on the wing is therefore somewhat subtle.
양력에 관한 Kutta-Joukowsky 이론에서는, 순환의 중첩이 이루어진다. 날개 위에서는 순환 속도가 날개를 지나 비회전 속도를 더하여 더 큰 속도를 낸다. 날개 아래에서는 순환이 비회전 흐름에 반대하며 공기 속도가 감소합니다.
베르누이의 원리에 따르면, 날개 위의 압력은 날개 아래의 압력보다 작기 때문에 양력이 있다.
따라서 날개에 양력을 얻는 데 베르누이 원리를 적용하는 것은 다소 미묘하다.
The actual lift on a wing is calculated in the Kutta-Joukowsky theory by determining the momentum change in the air
stream as it is deflected by the superimposed circulation. According to Newton's law, the force necessary to deflect the air
stream downward is equal to the lift on the wing. Some references erroneously describe lift on the wing but then show an air stream that leaves the wing moving in exactly its original direction.
날개의 실제 양력은 기류가 중첩된 순환에 의해 방향이 바뀔 때의 운동량 변화를 결정함으로써 Kutta-Joukowsky 이론에서 계산된다. 뉴턴의 법칙에 따르면, 기류를 아래로 꺾는 데 필요한 힘은 날개의 양력과 같다.
일부 참고문헌은 날개의 양력을 잘못 묘사하지만 날개가 원래 방향으로 정확히 움직이게 하는 공기 흐름을 보여준다.
'물리 > 유체역학' 카테고리의 다른 글
| [FC 4.38]건물 밑을 통과하는 바람 (0) | 2022.12.09 |
|---|---|
| 대류를 부력으로 설명하는 방법 (0) | 2019.05.07 |
| 베르누이 법칙과 역학적 에너지 보존 (4) | 2017.11.14 |
| [FC 4.21]공중에 떠 있는 공 (0) | 2017.09.07 |
| [FC 4.23]물에 의해 끌려오는 달걀 (0) | 2017.09.06 |